Música, Física y Matemáticas!

𝄞 Música, física y matemáticas 𝄞
Más cercanos de lo que parecen

La música es muy compleja, a pesar de que a simple vista no lo parezca. Tiene mucha relación con la física y las matemáticas debido a que la mayoría de los conceptos musicales se basan en ciertas partes de ambas materias ya mencionadas. Desde el concepto del sonido hasta la escala diatónica, las matemáticas y la física están presentes siendo partes fundamentales de lo que conforma la música.

Antes que nada, comencemos por saber qué es el sonido. Básicamente son ondas que se originan por la vibración de un cuerpo, estas ondas pueden ser percibidas o no por los seres vivos dependiendo de las características de dicha onda y de la afectación que ejerce sobre ella el medio por el cual se transmite. Siempre que haya ondas hay resonancia.
Resultado de imagen para sonido

La resonancia es un fenómeno en el cual un objeto resuena muy fuerte a una vibración que que se le ha introducido debido a que se ha dado con la frecuencia que encaja con su estructura y tamaño. De hecho, este fenómeno está en todas partes, por ejemplo cuando se toca cierta nota en un instrumento musical y vibra una puerta o cuando alguien rompe una copa con la voz, todo esto se produce gracias a que se toca la misma nota de aquel objeto y de esta forma vibra con mucha intensidad. La encontramos también en las resonancias magnéticas, ocurre lo mismo solo que en vez de sonido se tiene ondas electromagnéticas. 
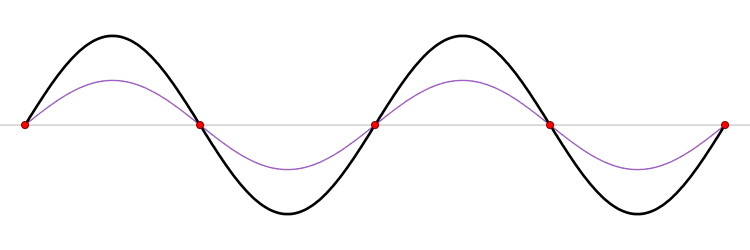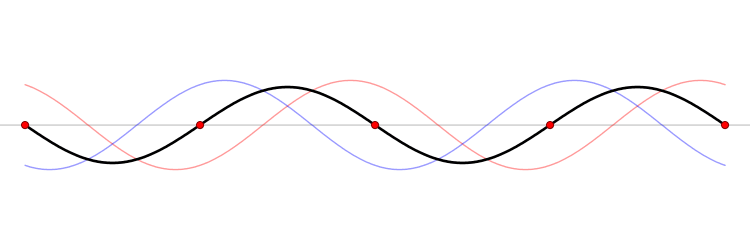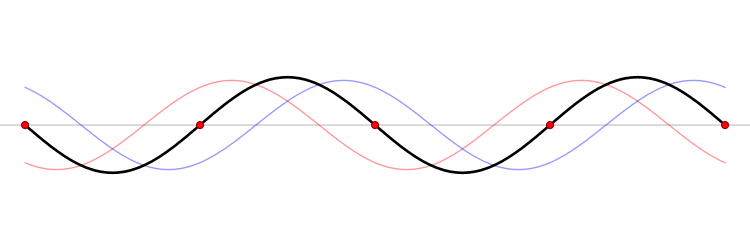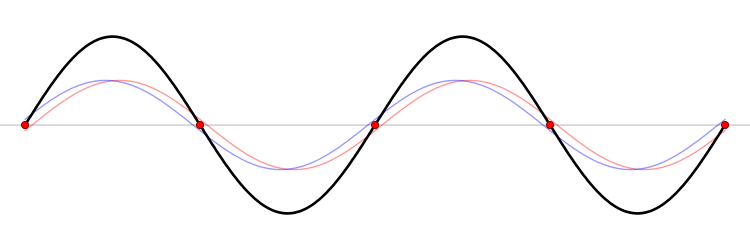
Resultado de imagen para resonancia del sonido gif"

Continuando con la resonancia, si se duplica la frecuencia se mantiene un punto intermedio quieto, donde se cancelan toda las vibraciones, llamado nodo. Este procedimiento se puede hacer sucesivamente, es decir, triplicando, cuadruplicando, quintuplicando, etcétera, de esta manera existen infinitas resonancias. A estas se les llama ondas estacionarias o modos vibracionales. La matemática dice que cualquier vibración que pueda realizar, por ejemplo una cuerda, se puede descomponer en una suma de todos los modos. Al primer modo se le nombra como frecuencia fundamental y al resto se les llama armónicos.
Resultado de imagen para resonancia del sonido"


Tomando esto en cuenta, encontramos que la sumatoria de todos los modos vibracionales es lo que reconocemos como una nota musical. Estas notas se pueden detallar en un espectro de frecuencia, en el cual se ven las ondas puras que se encuentran mezcladas dentro de una vibración más compleja, mostrando las frecuencias que predominan lo que se está escuchando.
Resultado de imagen para espectro de frecuencia"


 Matemáticamente se aplica una operación llamada Transformada de Fourier.


Ahora, con estas notas musicales se pueden formar ciertas escalas, por ejemplo la escala diatónica, construida por la escuela pitagórica al experimentar con las siguientes razones para expresar las longitudes de las cuerdas.


La escala usual es obtenida al tomar la quinta y la octava nota repitiéndolas de manera sistemática hasta que coincidan de nuevo, obtendremos que 12 quintas es igual a 7 octavas, es decir: (3/2)¹²: (2/1)⁷ = 1.0136...

 Esta diferencia condiciona las escala creando los modos mayores y menores. Posteriormente, un matemático francés llamado Marin Mersenne formuló precisamente la relación entre la longitud de cuerda y la frecuencia, haciendo que desaparecieran los problemas del reajuste de la afinación.


  • Ya con esta escala se pueden construir acordes, los cuales forman parte de lo que se conoce como armonía.
  • La escala puede ser modificada en una canción para crear una melodía, tocando una secuencia de notas de esta escala en un orden distinto.

Tanto la armonía como la melodía se visualizan en escrito, algo llamado partituras. Las partituras representan lo que hace cada instrumento, es decir las notas que se tocan en una composición en la cual habrá tantas partituras como instrumentos halla en la canción. En estas se encuentran las figuras, las notas, el tempo, las alteraciones, las armaduras de claves, entre otros elementos que permiten la interpretación de una pieza, ubicados sobre un pentagrama. Sobre este pentagrama, a la izquierda se coloca una clave que indica la tonalidad.
Resultado de imagen para partituras
Se dice que el "creador" de las partituras fue Guido d'Arezzo, un monje benedictino teórico de la música. De hecho él desarrolló el uso del tetragrama, que fue como el boceto del pentagrama sólo que en lugar de tener cinco líneas tenía cuatro, esto lo hizo con la intención de perfeccionar el lenguaje musical indicando las alturas en las que se ubican las notas de la escala diatónica. Además, d'Arezzo fue el que nombró a las notas de la escala como las conocemos utilizando la lógica, ya que se basó en el Himno a San Juan el Bautista en donde las notas van progresivamente, una más alta que la otra en la escala. Sabiendo esto, lo que hizo fue nombrar a cada nota como la inicial de cada línea de la letra del himno:"Ut queant laxis / Resonare fibris / Mira gestorum / Famuli tuorum / Solve polluti / Labii reatum / Santae Johannes". Siendo las notas "Ut, Re, Mi, Fa, Sol, La", a las que posteriormente se le agregó la séptima nota llamada"Si" y cambiando "Ut" a "Do".
Resultado de imagen para himno a san juan el bautista"
Entrando más a fondo en las matemáticas, hubo un hombre llamado Pitágoras, de seguro el nombre les suena. Él fue un filósofo y matemático griego, anteriormente se nombró la escuela que fundó, la escuela pitagórica, la cual no sólo aportó a las matemáticas sino que aportó a la música. Pitágoras introdujo la afinación pitagórica, siendo este el primer sistema de afinación documentado.
Resultado de imagen para pitágoras"
"Pitágoras deduce la razón matemática de los intervalos por medio de un instrumento llamado monocordio. Encuentra que al dividir una cuerda en dos partes iguales y comparar el sonido producido por una mitad con el de la cuerda en toda su extensión obtenemos el intervalo de octava." José Rodríguez Alvira (S.F.)
Al saber esto, Pitágoras llegó a la conclusión de que la razón matemática de la octava es 2 a 1. Hizo lo mismo dividiendo la cuerda en tres y en cuatro partes equivalentes, siendo la cuerda dividida en tres partes el intervalo de quinta, con razón de 3 a 2, y la cuerda dividida en cuatro partes la cuarta, con razón de 4 a 3. Con este sistema se construyó una escala mayor, partiendo de do multiplicando su frecuencia con el tamaño de la quinta. Luego se busca re desde sol, dividiendo la frecuencia de sol entre el tamaño de la cuarta. Así sucesivamente hasta obtener lo siguiente:




El único problema con este sistema es que al dividir la frecuencia de mi (330 Hz) entre la de do (261 Hz) quedaría una tercera más grande que la de la serie armónica, resultando 1,2643678161 en lugar de 1,25. De esta manera, quedaría desafinada. Gracias a este error se cambió a otro sistema de afinación: La Afinación Temperada.

Pasemos a la métrica musical.

La estructura organizativa básica de la música es el compás, integrado por un número  de unidades de medida o tiempos, estos van sucediendo uno tras otro creando así una cuenta en forma de ciclo, por ejemplo 1,2,3,4,1,2,3,4,1,2,3,4... Esto es un sistema de numeración con módulo n, en el cual n = 4 (en este ejemplo). Al codificar matemáticamente este fenómeno se puede aprovechar su identidad formal y funcional para resolverlo de forma matemática.
Resultado de imagen para metrica musical
De manera concluyente, podemos observar que tanto la física como las matemáticas se encuentran muy presentes en la música, desde números racionales hasta ecuaciones. Y estos son solo una pequeña parte de lo que conlleva la música, ya que existen una gran cantidad de términos musicales los cuales tiene también su explicación matemática, hablando de las medida del tempo, la formación de acordes, los diferentes signos, las escalas, entre otros. Así podemos notar que la música no es sólo algo que es agradable al oído, o algo que se compone para ser escuchado, sino que va más profundo siendo un lenguaje único, compuesto por varios elementos como la métrica, la melodía, la armonía, entre otros que se pueden codificar matemáticamente para entenderlos y analizarlos para comprender la música.

Si tienen cualquier aporte para esta investigación pueden ponerlo en los comentarios.

Fuentes consultadas: 

Comentarios

Publicar un comentario

Entradas populares